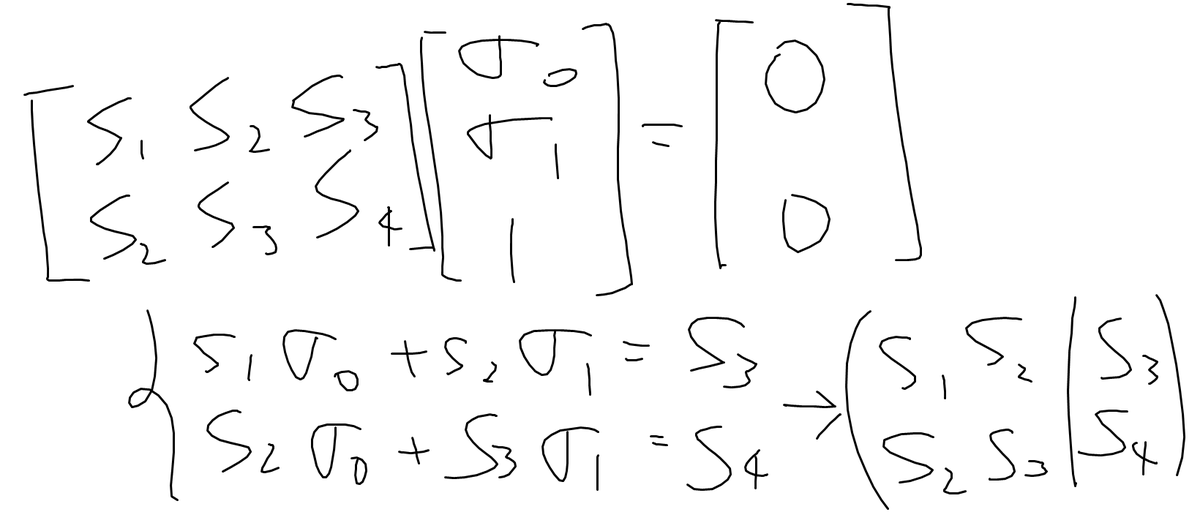この記事は呉高専アドベントカレンダー2022 11日目の記事です。
ごあいさつ
こんにちは、点Nです。電気情報 工学科卒です。高専 在学中は高専 プロコンに出たり、呉高専 史上初めてICPC (大学対抗競プロ合戦)に参加して予選敗退したりといった感じです。
アドベントカレンダー というと「(最新の何かすごい技術)を使って(こんな面白いもの)作ってみた!」みたいな(勝手な)イメージを持っているのでそういうキラキラした記事を書きたいところですが、あいにくそういうのは性に合わないので黒い画面に白い文字が出るタイプのプログラミングをやります。タイトルにもある通り車輪の最発明をやりますので、みなさんは僕が車輪を最発明しているようすを見ていてください。目次の長さや画面右のスクロールバーの大きさから察している方も多いと思いますが、この記事はめちゃくちゃ長いです。せっかくの日曜日ですが(なので)、どうか最後までお付き合いください。
注意点
素人プログラミング
ふわふわ理論
ガタガタ構成
エンドレス文章
それでもOKな人はどうぞ
はじめに
(呉高専 アドベントカレンダー なので、高専 を絡めた導入をどうにか考えました。)
高専 といえばロボコン 。世の中そういうイメージの人が大半ですが、高専 にはそれ以外のコンテストもあります。代表的なところでは、ごあいさつで述べた高専 プロコンというプログラミングの大会が有名です。その中の競技部門という部門では与えられた課題(対戦ゲームや一人用ゲームなど)を解くプログラムの強さを競います。しかしこの部門、稀に「プログラミングするより人間がやったほうが強い」という現象が起こることがあります。例えば、第23回有明 大会の競技課題は「サイコロの山を見てその数を数える」というものでしたが、上位の成績を収めた多くのチームが(画像処理ではなく)人の目でサイコロを数えるという手段をとったそうです。
第27回鳥羽大会でも似たようなことが起きました。競技内容は木製のジグソーパズルが(現物で!)与えられるので解け、というものでした。パソコンにピースの形状を読み込ませ、正しい配置を探索するというのが正攻法なのですが、それでも解くのが難しく、また外枠内に収めたピースの数で評価したために「最大のピースを諦めて残りを人が急いで詰め込む」という計算機完全無視の手段がかなり強くなってしまいました。実際、翌年の募集要項に「昨年の大会では,手でパズルを並べると上位に来ることができました」という記述があります(https://www.procon.gr.jp/wp-content/uploads/2017/04/8db30280f6638520be40ad86b4bf1b37.pdf )。
勘のいい人はお分かりかと思いますが、募集要項にこのようなことが書かれた第28回大島大会の競技課題は、第27回の競技課題をアレンジしたものでした。競技者はペナルティを支払うことでパズルを解くヒントを利用することができるようになり、ヒントを使ってでも「パズルを完成させる」ことを重視する評価基準になりました。そして、ヒントは紙に印刷されたQRコード で配布されました。仕組みを理解していれば不可能ではないのですが、よほどの天才でない限りQRコード は人力では読めないので、さすがにプログラミングをせざるを得ません。
高専 プロコンの話はこれぐらいにして、本題に入ります。このQRコード 、多少汚れるなどしていても読み取れるのをご存知でしょうか。これは本来のデータだけでなく、いっしょに「データが壊れた時に気付いて、元に戻すための手がかり」も記録しておくことにより、汚れなどで欠けた部分を補って正しいデータを復元できるようにしているためです。
これを実現するための具体的なやり方はいろいろありますが、QRコード ではリード・ソロモン符号というものを用いています。今回はこの符号を最発明します。といっても理論を思いつくのは不可能なので、意図的に壊したデータを頑張って復旧させるプログラムを書きたいと思います。
余談:人力という戦略について
人の力に頼ること自体は悪いことではありません。人もシステムの一部とみなして有効に使うことで非常に優れた問題解決能力を実現できる場合があります。例えば、第30回都城 大会の競技課題は陣取りゲーム形式の通信対戦ゲームでした。1ターンの時間は数秒から十数秒と短く、人力で最大8人もの味方の動きを制御するのは難しいため、基本的にはコンピュータが考えることになります。しかし、味方全員は不可能であっても、その中の一人か二人程度であれば、その動きを人が決定することが可能です。「シンプルな戦略に則ってコンピュータが個々の味方の行動を計算、人間は必要があればそれを修正し、大局的に見てより良い手を柔軟に選択できるようにする」という方針をとった東京高専 はこの年の競技部門で優勝しました(というかこの年は東京高専 が3部門全てで優勝したのですが)。
当時の東京高専 の学生によるツイート:
shibh308 on Twitter: "#procon30 深夜になってしまいましたが、東京高専競技部門の方針について説明します" / Twitter
計算能力ではパソコンに遥かに劣りますが、人の力も決して弱くはありません。問題を人力で解くことが十分強いのであればそれも立派な戦略だと思います。プログラミングの大会としてコンピュータを一切使わないのが最適ってのはいかがなものかと思いますが。
ふんわり理解するリード・ソロモン符号
リード・ソロモン符号(Reed-Solomon Coding, RS符号)はリードさんとソロモンさんが考えた誤り訂正符号(データにくっつけておくことでデータに発生した間違いを発見し、直せる符号)です。QRコード をはじめ、Blu-ray ディスク、地デジ放送、ADSL その他諸々に応用されています。この世界はリード・ソロモン符号なしには成り立たないと言っても過言ではありません。ちなみに背景にある数学的な理論はちゃんと難しいです。
符号化・復号の流れ
いったん、細かい話は抜きでざっくり書きます。かなり説明不足で厳密性に欠けます。
符号化
線形代数 の気持ちになります。小文字がベクトルで大文字が行列です。まず元の情報
復号
壊れている可能性のある、ローム と呼ばれます。
そのために、ローム 行列多項式
忙しくない人と僕のためのRS符号の理論
実装するだけなら理解しなくても大丈夫ですが、RS符号がなんなのか全く分かっていないのもまずいので、ここでRS符号とはつまり何なのかについて知っておきたいと思います。適宜飛ばしてください。僕の理解が足りないので、間違った記述も含まれていると思います。
そもそもRS符号は何がすごいのか
とにかく訂正能力が高いです(そのぶん処理はやや複雑です)。正しいかは素人なので判断できませんが、僕は「理論値じゃん」という印象を受けました。
まず、符号どうしの 距離を考えます。符号の最小距離うしの ハミング距離の最小値です(ハミング距離は違っている場所の数です。たとえば、"abcde "と"abcxy "という符号のハミング距離は2です) 。距離の小さい、つまり似たような符号があると、ちょっとしたエラーが発生するだけでそれらを間違えてしまいそうです。なので、
しかし当然ながら
ここがすごいところなのですが、RS符号は、最小距離がシングルトン限界
RS符号は
RS符号とは
ずばり、こういうものです。
多項式 の集合
(参考書籍[1] p.63, 定義 4.1.1)
長さ多項式 のうち、次数が多項式 に代入していった結果を並べて多項式 に同じことをして得られる符号語の集合がRS符号ということです。
あるメッセージと対応する符号語の関係をざっくり言うと、符号語は「メッセージを多項式 関数に置き換え、1から順に数を代入した結果の一覧」です。符号化はこの一覧表の作成をやるだけです。復号は結果一覧から多項式 関数を特定する作業になります。多項式 が違えば結果はある程度異なるものになるので、結果一覧に誤植があっても、少しなら問題ありません(誤り訂正)。
素数 のべき乗なら何でもよいのですが、実用上は
なぜ体が出てくるのか
なぜ文字をそのまま0から255までの整数だけの世界(256で割った余りの世界/mod 256の世界) で考えようとしないのかですが、それだと困ることがあります。加減算と乗算はよい(結果を256で割った余りに置き換えれば0~255の範囲に収め直せる) のですが、割り算が困ります。なんと割り算ができないことがあります(例えばmod 256の世界に2x=1を満たすxは存在しません、これはmod 非素数 の世界を考えた時に起こります) 。この先で割り算を使うので、四則演算ができる体、特に要素が有限で閉じている(演算結果も必ずその体の要素な) もの(=有限体/ガロア 体)の世界で考える必要があります。
原始元とは
体の元であって、
RS符号の世界(ガロア 体)について
素数 がガロア 体とか有限体と呼びます。
ガロア体の例
最も簡単なガロア 体は、ずばり、1bitの世界、0と1の世界です。
この加減算は排他的論理和 (xor)という演算で、0どうし1どうしでは0に、0と1では1になります。プログラミング言語 でもこの演算が(大抵)サポートされていて、(大抵)^という演算子 を使います。
同様に、素数 ガロア 体
ガロア拡大体(今回扱う体の話)
ガロア 体ガロア拡大 体
多項式 の係数だと思うことにします。多項式 (=因数分解 できない) 多項式 )とします。
(ここから今回の多項式 という既約多項式 で、この根(多項式 に代入すると0となる解)は原始元多項式 の根なので多項式 的には、乗算のmodをこの多項式 にします。
結局、こんな感じになります。
体の元とbit列、多項式 は次の表のような対応をします。
元
対応するbit列
多項式 としての解釈
00000000
0
00000001
1
00000010
00000100
00001000
10000000
00011101
00111010
符号化
前提を再掲します:
符号化は、長さ多項式
生成行列と検査行列
生成行列フーリエ変換 そのものっぽいです(参考[6])。
検査行列
理由
実際に計算してみるとわかります。等比数列 の和の公式より
ローム はローム はどうなっているかですが、あるエラー
エラー検出:ピーターソン法
復号のアイデア は以下の通りだそうです。正直僕はあまり理解できてないです。
イデア は,2変数多項式
であって,以下の条件を満たすものを決定することである.
(参考書籍[1], p.65)
本文中で使ってきた多項式 があることがいえます。
また、この方程式に関して次の定理が成り立ちます。
送信語が
(参考書籍[1], p.65, 定理4.2.2)
なぜ?
参考書籍[1], p.65, 定理4.2.2の証明に基づく説明です。
恒等的に
「送信語が多項式 の次数は条件2,3より高々
エラーの位置は( 。この性質から多項式 と呼ばれます。
以後
さて、ここから復号までには何通りかの方法があります。ここではピーターソン法と呼ばれる方法を取り上げます。この方法ではまずエラー位置特定(
第一段階、エラー位置特定です。次の定理を用います。(
誤り位置多項式
(参考書籍[1], p.72, 定理4.4.1)
本当に?
参考[1] pp.72-74の証明にもとづいて説明をします。
両辺に左から次の行列をかけると、(生成行列に検査行列をかけたのと同様の原理で)左辺第一項が消えます。
残った左辺第二項は、次のように変形できます。
あとは、
であることを確認します。行列を分解したことで計算が簡単になって、右辺の計算結果は
になることが確認できます。いっぽう、左辺については
であることから一致します。
証明は省きますが、
第二段階です。
最後に方程式
実装
さて、だいぶ理論の話が長くなりましたが、ここから実装していきます。実装してから理論を書いたので若干記号が違ったりします。
何をするか
ユーザの入力:ASCII文字列
プログラムから見た入力:
出力:もとのメッセージ
手抜きPoint
今回はエラーがひどすぎて復元できない場合を想定しません。めんどくさいし、復号できないことがわかっても嬉しくないし、直せるものがきちんと直せると分かればいいので。
ヒントとして、元のメッセージの文字数は復号プログラムに教えます。固定長になるように分割したり付け足したりするか、特定の書式を用意したりすれば解決するのですが、そこは面白くない場所なので。
計算資源に関する制約はあまり意識しません。最良の方法であることよりも実装の手軽さなどを優先し、一般的な家庭用のパソコンで実行したときに即座に実行が完了する程度に動けばよいことにします。
入力
入力された一行のメッセージgetline()で受け取ります。cinは空白で区切られてしまうので不便です。符号化したメッセージもっというと破壊したいので ここではとりあえず200文字以内のメッセージなら受理ということにします。自分が使うプログラムなので基本的には性善説 に基づいた実装ですが、いちおう長すぎる入力や空の入力は弾くようにします。僕の環境ではどうにかなるようですが、マルチバイト文字は入れないでほしいです。
ついでにstoi()様の解釈を正義とします。エラーの場合は再入力です。データを破壊しないこと、つまり
const string input = Input::getRangeString ("Input the string (<=" +to_string (maxK)+" letters)" ,1 ,maxK+1 );
const int K = input.size ();
const int maxChange = (N-K)/2 ;
const int change = Input::getRangeNum ("Input the number of data to be corrupted (<=" +to_string (maxChange)+")" ,0 ,maxChange+1 );
Input::xxx
namespace Input{
bool inRange (const int n, const int l, const int r){
return l<=n&&n<r;
}
bool isRangeNumStr (const string & s, const int l, const int r){
int a;
try { a = stoi (s); }
catch (...){ return false ; }
return inRange (a,l,r);
}
string getRangeString (const string & message, const int l, const int r){
string S;
while (true ){
cout << message << endl ;
getline (cin ,S);
if (inRange (S.size (),l,r)) return S;
}
}
int getRangeNum (const string & message, const int l, const int r){
string numString;
while (true ){
cout << message << endl ;
getline (cin ,numString);
if (isRangeNumStr (numString,l,r)) return stoi (numString);
}
}
}
拡大体
(筆者は論理シフトと算術シフトの違いで痛い目を見たことがあります) のでunsignedです。ここに加減乗除 を定義します。演算子 オーバーロード というやつです。これにより(ソースコード 上で)普通の整数と同様に扱うことができます。
配列A[256]を用意し、Aを参照することで
加減算はbitwise xorなので^演算子 を用いてシンプルに書けます。
乗除算も頑張ればbit演算でできる気がしますが、簡単な方法でやります。まず、0が絡む場合は場合分けして個別に処理します。それ以外は肩の数字のmod 255での加減算になります。各元は自分が
alpha
剰余をとるのは負の数を正の数に直してから。一部省略していますが、実際は複合代入演算子 (+=など)も定義しています。
struct alpha{
unsigned char v;
alpha ():v (0 ){}
alpha (unsigned char a):v (a){}
const alpha operator + (const alpha& r) const { return alpha (v^r.v); }
const alpha operator - (const alpha& r) const { return alpha (v^r.v); }
const alpha operator * (const alpha& r) const {
if (*this ==0 || r==0 ) return 0 ;
int expL = revA[v], expR = revA[r.v];
return A[(expL+expR)%255 ];
}
const alpha operator / (const alpha& r) const {
assert (r!=0 );
if (*this ==0 ) return 0 ;
int expL = revA[v], expR = revA[r.v];
return A[(expL+255 -expR)%255 ];
}
static alpha pow (int x){
if (x<0 ) x+=((-x)/255 +1 )*255 ;
return A[x%255 ];
}
static array <alpha,256 > A;
static array <unsigned char ,256 > revA;
static void initialize (){
A[255 ]=0 ;
revA[0 ]=255 ;
for (unsigned char i=0 ;i<8 ;i++){
A[i]=1u <<i;
revA[A[i].v]=i;
}
for (unsigned char i=8 ;i<255 ;i++){
A[i]=A[i-4 ]+A[i-5 ]+A[i-6 ]+A[i-8 ];
revA[A[i].v]=i;
}
}
}
あと、後々面倒なのでalphaのベクトルや行列、すなわちvector<alpha>やvector<vector<alpha>>は略記ができるようにしておきます。
using Vec = vector <alpha>;
using Matrix = vector <vector <alpha>>;
符号化
生成行列
vector )を作るだけなのでプログラミング的な面白さはないです。
const Matrix G = RS::MatrixGen::Generate (K,N);
RS::MatrixGen::Generate
Matrix RS::MatrixGen::Generate (const int K, const int N){
Matrix G (K,Vec (N));
for (int k=0 ;k<K;k++) for (int n=0 ;n<N;n++) G[k][n] = alpha::pow (k*n);
return G;
}
符号語生成
const Vec message = RS::MatrixGen::message (K,input);
const Vec word = Math::mul (message,G);
RS::MatrixGen::message, Math::mul
Vec RS::MatrixGen::message (const int K, const string & S){
assert ((int )S.size ()==K);
Vec word (K);
for (int i=0 ;i<K;i++) word[i] = S[i];
return word;
}
Vec Math::mul (const Vec& a, const Matrix& M){
int H = M.size (), W = M[0 ].size ();
Vec res (W);
for (int i=0 ;i<W;i++) res[i] = 0 ;
for (int y=0 ;y<H;y++) for (int x=0 ;x<W;x++) res[x] += a[y]*M[y][x];
return res;
}
データ破壊
const Vec brokenWord = RS::MatrixGen::errorMessage (word,change);
RS::MatrixGen::errorMessage
そうする意味は特にないのですが、アルゴリズム の癖として、連続した場所を破壊する傾向にあります(既に破損させた場所を再選択した場合に右方向で最も近い未破損データを壊すため)。
mt19937 mt (chrono ::system_clock ::to_time_t (chrono ::system_clock ::now ()));
uniform_int_distribution <int > distN (0 ,N);
uniform_int_distribution <unsigned int > dist255 (0 ,256 );
Vec RS::MatrixGen::errorMessage (const Vec& word, const int change){
Vec brokenWord (word);
vector <bool > changeFlag (N,false );
for (int i=0 ;i<change;i++){
int pos = distN (mt);
while (changeFlag[pos]) pos=(pos+1 )%N;
changeFlag[pos] = true ;
alpha after;
do { after = dist255 (mt); } while (after==brokenWord[pos]);
brokenWord[pos] = after;
}
return brokenWord;
}
符号語比較
人間が見てわかるようにここで
符号語表示
alpha型の中身はunsigned char型の変数ですが、文字としてそのまま出力することはできません(ASCIIが対応するのは0-127までなので範囲外になることがあり、かつ範囲内にも改行やヌル文字などの表示できない文字=制御文字がある) 。unsigned charが扱う0~255の値を2桁の16進数(適宜0埋め)に変換して表示します。
表示
ostream & operator << (ostream & ost, const alpha& a){
return ost << hex << setw (2 ) << setfill ('0' ) << (int )a.v << setfill (' ' ) << dec ;
}
ostream & operator << (ostream & ost, const Vec& v){
for (auto itr=v.begin ();itr!=v.end ();itr++) ost << *itr;
return ost;
}
比較
上の要領で符号語を人に読める文字にできますが、ふたつの符号語を上下に並べて表示したとして、それを比較するのはおよそ人間のやることではありません。違っているところを目立たせるために、文字と背景の色を反転させます。coutで出力するとき、\033[7mを噛ませることで反転、\033[0m=\033[mで戻すことができます(参考:
もう一度基礎からC言語 第47回 特殊な画面制御~コンソール入出力関数とエスケープシーケンス エスケープシーケンスによる画面制御
)。
compare (word,brokenWord,"Original" ,"Broken" );
compare
せっかくなので符号語以外のvectorも対応できるようにしておきます。
template <typename T>
void compare (const vector <T>& A, const vector <T>& B, const string & s1, const string & s2){
assert (A.size ()==B.size ());
const string flip = " \033 [7m" ;
const string endFlip = " \033 [m" ;
cout << endl ;
cout << "------compare------" << endl ;
int N = A.size ();
vector <int > dif;
cout << s1 << ':' << endl ;
cout << A << endl ;
cout << s2 << ':' << endl ;
for (int i=0 ;i<N;i++){
if (A[i]==B[i]) cout << B[i];
else {
dif.push_back (i);
cout << flip << B[i] << endFlip;
}
}
cout << endl ;
if (dif.empty ()) cout << "No error." << endl ;
else cout << "Error at:" << dif << endl ;
cout << "-------------------" << endl << endl ;
}
検証
検査行列
誤り検出に使用します。転置した状態で使うので最初から転置した状態の
const Matrix H = RS::MatrixGen::Check (N,N-K);
RS::MatrixGen::Check
Matrix RS::MatrixGen::Check (const int N, const int NK){
Matrix H (N,Vec (NK));
for (int n=0 ;n<N;n++) for (int x=1 ;x<=NK;x++) H[n][x-1 ] = alpha::pow (n*x);
return H;
}
ローム を計算します。符号語を生成したときと同じ要領なので同じ関数を使いまわします。結果が
const Vec syndrome = Math::mul (brokenWord,H);
Vec restoredWord (word);
if (!Math::isZeroVec (syndrome)){
const vector <int > errorPos = RS::specifyError (maxChange,syndrome);
restoredWord = RS::restoreWord (brokenWord,errorPos,H,syndrome);
}
else { cout << "Data is not broken." << endl ; }
エラー処理
RS::specifyError
vector <int > RS::specifyError (const int maxChange, const Vec& syndrome){
Matrix S = RS::MatrixGen::Syndrome (maxChange,maxChange+1 ,syndrome);
const int rnk = Math::gauss_jordan (S);
const Vec sigma = MatrixGen::sigma (rnk,S);
return RS::findErrorPos (sigma);
}
RS::MatrixGen::Syndrome
Matrix RS::MatrixGen::Syndrome (const int H, const int W, const Vec& syndrome){
Matrix S (H,Vec (W));
for (int y=0 ;y<H;y++) for (int x=0 ;x<W;x++) S[y][x] = syndrome[y+x];
return S;
}
const int rnk = Math::gauss_jordan(S);)。下の
掃き出し法を使った後の多項式 const Vec sigma = MatrixGen::sigma(rnk,S);)。
RS::MatrixGen::sigma
Vec RS::MatrixGen::sigma (const int rnk, const Matrix& S){
Vec sig (rnk+1 );
for (int y=0 ;y<rnk;y++) sig[y]=S[y][rnk];
sig[rnk] = 1 ;
return sig;
}
理論と言ってることが微妙に違いませんか
文献[4]を参考に、エラー個数と誤り位置多項式 を一気に求める方法をとっています。
ここから適当なことを言うのですが、根を求めるだけなので、誤り位置多項式 には適当な定数をかけてよく、最高次の係数を1にすることができます。その状態から変形すると掃き出し法に持っていける感じがしてきます。
こう
で、見つかるまで次数をあげていきながら多項式 を求めている、という感じの処理になっている(のだと思っていますが、厳密な原理は参考元をあたってください)。
RS::findErrorPos(sigma);)。
RS::findErrorPos
vector <int > RS::findErrorPos (const Vec& sigma){
vector <int > errorPos;
for (int j=0 ;j<N;j++){
if (Math::polynomial (sigma,alpha::pow (j))==0 ) errorPos.push_back (j);
}
return errorPos;
}
alpha Math::polynomial (const Vec& coef, const alpha a){
alpha x (1 ), sum (0 );
for (const alpha& c:coef){
sum += c*x;
x *= a;
}
return sum;
}
今回は排除しているので心配いりませんが、一般に多項式 の根が見つからなくなるようです(参考:文献[4])。
掃き出し法
掃き出し法の実装がプログラム全体で最も難しいと思います。とはいっても、今回は誤差やオーバーフローの心配がなく、その点ではやや簡単ともいえます。基本的には人間がやるような感じをプログラムに書き直すだけです。
具体的な手続き
大まかな流れを記述します。行列
その列にゼロでない要素
見つかったら、行
行
行
プログラムは雑に書くとそれ以降も参照する必要のある変数をうっかり書き換えてしまうバグを埋め込みやすいです。
Math::gauss_jordan
一部の処理の順番を入れ替えてあります。
int Math::gauss_jordan (Matrix& A){
const int H = A.size (), W = A[0 ].size ();
int rnk=0 ;
for (int x=0 ;x<W;x++){
for (int y=rnk;y<H;y++){
if (A[y][x]!=0 ){
if (y!=rnk){
swap (A[y],A[rnk]);
y=rnk;
}
const alpha ayx = A[y][x];
for (int xx=0 ;xx<W;xx++){
A[y][xx] /= ayx;
}
for (int yy=0 ;yy<H;yy++){
if (yy==y) continue ;
const alpha f = A[yy][x];
for (int xx=0 ;xx<W;xx++){
A[yy][xx] -= A[y][xx]*f;
}
}
rnk++;
break ;
}
}
}
return rnk;
}
エラー除去
未知数が減ったので、方程式
RS::restoreWord
Vec RS::restoreWord (const Vec& brokenWord, const vector <int >& errorPos, const Matrix& H, const Vec& syndrome){
Matrix ErrorEquation = RS::MatrixGen::ErrorEq (errorPos,H,syndrome);
Math::gauss_jordan (ErrorEquation);
const Vec error = RS::MatrixGen::error (errorPos,ErrorEquation);
return Math::sub (brokenWord,error);
}
Matrix RS::MatrixGen::ErrorEq (const vector <int >& errorPos, const Matrix& H, const Vec& syndrome){
int error = errorPos.size ();
Matrix E (error+1 ,Vec (H[0 ].size ()));
for (int i=0 ;i<error;i++) E[i] = H[errorPos[i]];
E[error] = syndrome;
return Math::transpose (E);
}
Vec RS::MatrixGen::error (const vector <int >& errorPos, const Matrix& E){
vector <alpha> err (N,0 );
int e = errorPos.size ();
for (int i=0 ;i<e;i++) err[errorPos[i]] = E[i].back ();
return err;
}
メッセージ復号
遥か昔のことなので忘れそうですが、連立方程式 を解きます。これも掃き出し法で解けます。最後に復号したメッセージを出力して比較すれば無事return 0;です。
const string output = RS::decode (G,restoredWord,K);
cout << "Restored your input: " << output << endl ;
compare (vector <char >(input.begin (),input.end ()),vector <char >(output.begin (),output.end ()),"Original message" ,"Recovered message" );
return 0 ;
RS::decode
string RS::decode (const Matrix& G, const Vec& word, const int K){
Matrix Gw = Math::AugCoef (G,word);
Math::gauss_jordan (Gw);
string message = "" ;
for (int i=0 ;i<K;i++) message += Gw[i].back ().toChar ();
return message;
}
全体実装はそれなりに長いのでリンクを貼ります。
reedsolomon.cpp - Google ドライブ
動作確認
プログラムを動かしてみて、誤り訂正できていることを確かめました。僕の環境はC++ 14ですがC++ 11でも動くと思います。実行する場合は画面処理(文字色と背景色の交換)があるので対応できる環境で。Windows のコマンドプロンプト ではうまくいきません。どうにかできるとは思いますが、おとなしくPowerShell とかWSLを使ったほうが手っ取り早いと思います。
かなり見づらい実行画面
おわりに
リード・ソロモン符号(のおいしいところだけ、ですが)を実装してみました。何かの役に立つわけでもないし、画面に文字が並ぶだけで見栄えもしませんが、我々の生活を陰で支えるアルゴリズム に目を向けて、実装してみるのもけっこう面白いと思います。それでは。
XXXXXX_XXX_XXXXXXX_XX_XXX_XXXX_XXXXX
209be895e02f0bfdfc911a984fc51f516687cb55ce343c3c38b806c0a72b0a371f012706e6adc468c2a1ad20891f107d647b3b5935e9137aaace5db2fcd1164b9df34c3102c10dbd317af006ec43ea45e5c5c0ef28c7dfb606071457244d31c345a83df373d6aac8f0139b05bb84dd4aa3fb21c3742d5fe3dcefec442a1f01e2f5ba4d11f909ffe5ebdbfef722ad5fc15e0ed2160d5753ae08c9de9fa58ebd9c46fc8753d2cb5c92cf15f638d0796efddfd60b3fd89e5f6bdcc25940777b32343fdc677fa4bb98d42cefe74c18f15c190846f6fb32dd0489d296154aedd499c140936a8768e04470e70a5a0252413c6855df9604b895ccf44fee14fa103b5a
おまけ
当初は高専要素皆無だった導入部分(こっちのほうが自然でいいと思う)
情報は、時に欠落や破損をしてしまうものです。手の甲のメモが消えて読めなくなってしまったり、「ニンニク増しで」って言ったのに「ニンニク無し」が出てきたり、(この先は血で汚れていて読めない)
しかし、頑張ればなんとかなるケースも多々あります。なんか文字化けし縺ヲ繧けどギリギリ読める、誤字脱字がるけど陽はこういう意味だよな、と人間の脳は情報を補完します。
同じことをコンピュータの世界でもやっています。QRコード は多少汚れていても読めるし、ディスクに多少傷がついていてもCDは再生できます。必要なデータだけでなく、いっしょに「データが壊れた時に気付いて、元に戻すための手がかり」も記録しておくことで欠けた部分を補っているのです。
具体的なやり方はいろいろあり、その一つにリード・ソロモン符号というものがあります。今回はこれを最発明します。といっても理論を思いつくのは不可能なので、意図的に壊したデータを頑張って復旧させるプログラムを書きたいと思います。
参考文献
[1] 誤り訂正符号入門(第2版), イエルン・ユステセン, トム・ホーホルト原著, 阪田省二郎, 栗原正純, 松井一, 藤沢匡哉 訳, 森北出版(2019)
[2] 有限体(ガロア体)の基本的な話 | 高校数学の美しい物語
[3] 有限体でのガロア拡大(その3) - zuruyasumineko2002’s blog
[4] QRコード の符号化・復号アルゴリズム 解説:学習読み物としての試み, 佐藤創, 専修大学 情報科学 研究所所報,76,37-52 (2011-06-30)
[5] Reed-Solomon符号を15分で理解する【M3 Tech Talk 第187回】 - YouTube
[6] リード・ソロモン符号とその復号法, 松嶋敏泰, 映像情報メディア学会誌 Vol. 70, No. 4, pp. 571~575(2016)
https://www.jstage.jst.go.jp/article/itej/70/7/70_571/_pdf